Dijkstra

Dijkstra(다익스트라)

• Dynamic Programming을 이용한 최단경로 알고리즘
• 특정 노드에서 다른 나머지 노드로 가는 최단경로를 구할 때 사용
• 첫노드부터 모든 노드의 최단거리 저장하는 배열 및 우선순위큐 사용

Dijkstra 알고리즘 순서

1. 노드의 개수만큼 distances 생성, 시작 노드의 값은 0

2. 우선순위 큐 생성 및 첫노드 가중치 0

3. 우선순위큐에서 추출된 노드와 연결된 인접 노드와의 거리 + 추출된 노드 가중치를 계산하여

    distances의 값보다 적으면 distances업데이트 및 우선순위큐 insert

 

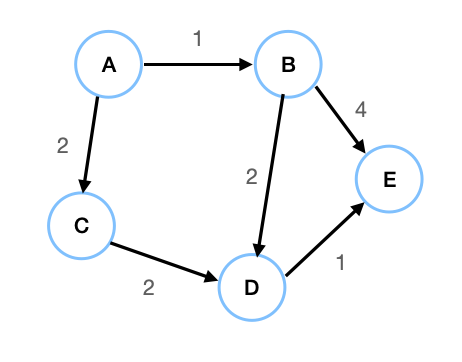
구현 코드

struct NodePriority: Comparable {
    var node: String = ""
    var priority: Int = 0

    static func < (lhs: NodePriority, rhs: NodePriority) -> Bool {
        return lhs.priority > rhs.priority
    }
}

func dijkstra(start: String, graph: [String: [String: Int]]) -> [String: Int] {
    var distances: [String: Int] = [:]
    var priorityQueue = Heap(elements: [NodePriority(node: start, priority: 0)], sort: >)
    let INF = 987654321
    
    for node in graph.keys {
        if node == start { distances[node] = 0 }
        else { distances.updateValue(INF, forKey: node)}
    }
    
    while priorityQueue.elements.count > 0 {
        guard let poppedValue = priorityQueue.pop() else { break }
        
        if distances[poppedValue.node]! < poppedValue.priority {
            continue
        }
        
        for (node, priority) in graph[poppedValue.node]! {
            let distance = priority + poppedValue.priority
            if distance < distances[node]! {
                distances[node] = distance
                priorityQueue.insert(NodePriority(node: node, priority: distance))
            }
        }
    }
    
    return distances
}

let graph: [String: [String: Int]] = [
    "A" : ["B": 1, "C" : 2],
    "B" : ["D": 2, "E": 4],
    "C" : ["D": 2],
    "D" : ["E": 1],
    "E" : [:]
]

dijkstra(start: "A", graph: graph) // ["A": 0, "B": 1, "C": 2, "D": 3, "E": 4]

 

참고 출처 : https://babbab2.tistory.com/110